Rational Scale

A standard Chromatic scale widely used in music today has a limitation that it can not represent harmonic series exactly. Harmonic series is derived from the physics of resonating strings, which produce fundamental frequencies as well as overtones, or harmonics. The frequencies of harmonics differ by integer multipliers (i.e. 2,3,4,5,...). These harmonics superimpose to produce frequencies that differ by various fractions build of integer numbers, such as 1/2, 2/3, 3/4, 4/5, 5/6, ... as well as 3/2, 4/3, 5/4, 6/5, etc. By definition, these fractions represent subsets of rational numbers.

When the frequencies of sounds relate to each-other through such harmonic multipliers they tend to produce pleasant sound combinations. For example, if the fundamental frequencies of three sounds build a ratio like:

They will sound like a major chord in chromatic scale, e.g. C,E,G. The important word here is like. The actual major chord ratio will be:

where the long numbers above are the result of logarithmic operation, and are in fact transcendental, as the famous number PI. This difference does not seem to be significant. However, for a minor chord it will be greater:

And the closest rational ratios are:

And other tones in a chromatic scale tend to deviate even further from rationality which is shown in the plot below:

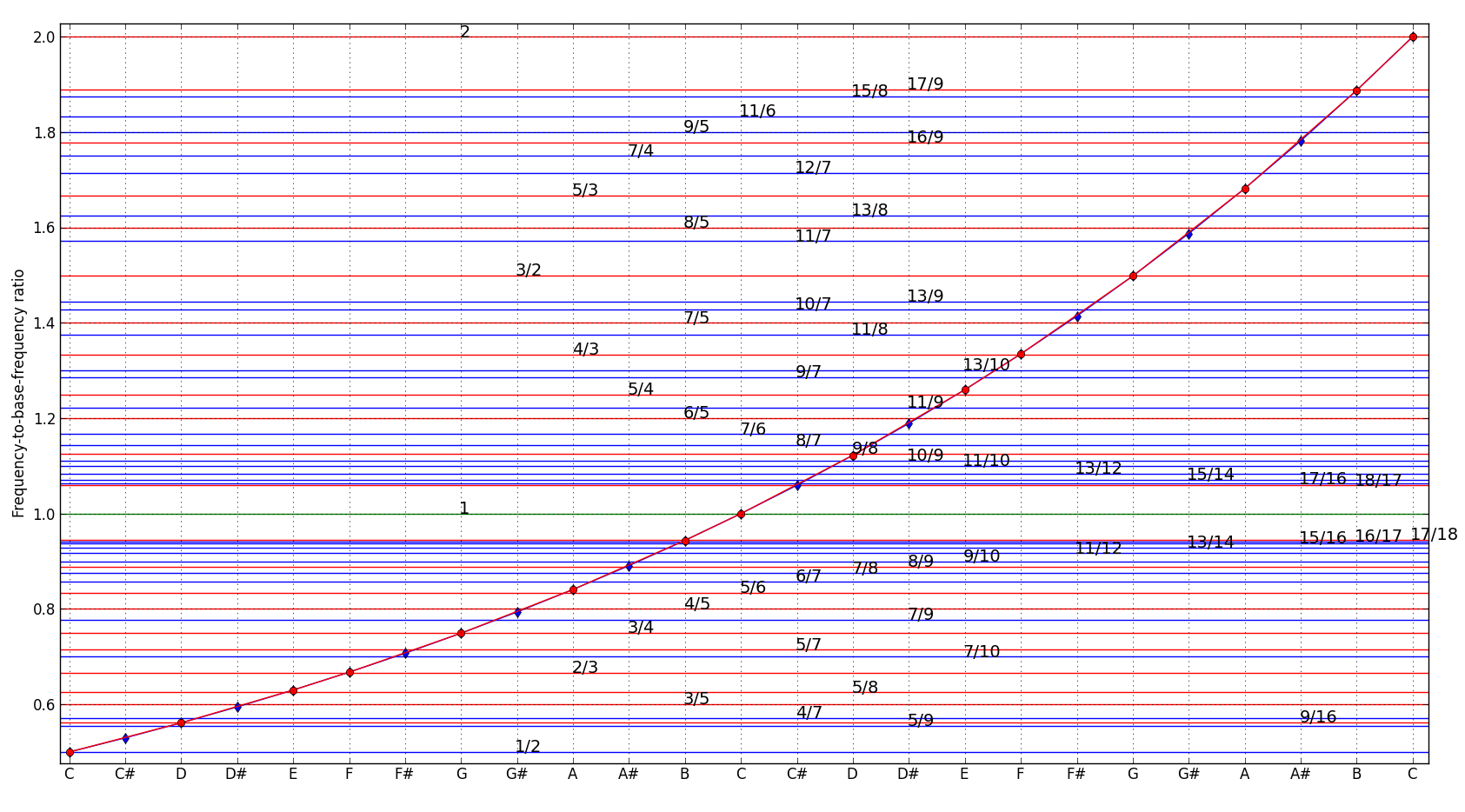
where red dots on the curve indicate the tones of major chromatic scale in C-key. As can be seen, frequencies derived from rational numbers, built on simple ratios, which we shall call a rational scale, rarely agree with the frequencies of the chromatic scale. This is one of the reasons why chords played on an electronic keyboard sound less pleasant than those played on an acoustic piano. Acoustic strings can experience resonance effect. As a result of this they can self-adjust their frequencies to each-other, thereby deviating from chromatic tuning to a more pleasant rational intervals.

The discovery of rational scale is attributed to an ancient Greek mathematician Pythagoras who used a specific subset of rational numbers known as a Pythagorean scale. The earlier instruments were built on that scale. However, it also has a problem. Namely, the scale built on rational numbers is not uniform across the octaves. Octaves are the frequency ranges scaled by the factor of the power of two, i.e. 2ⁿ, with n being an integer number like: -4,-3,-2,-1,0,1,2,3,4, which will produce 9 octaves. If one wants to play an instrument with multiple octaves, or just in different keys, and retain similar sound combinations of tones in each octave, one can not easily accomplish this with a rational scale. This can be seen in the plot above. In other words, in Pythagorean scale the same melody played in different keys will not sound the same.

That's why chromatic scale was discovered as a practical means to build a key-based instrument. Thus, chromatic scale is a compromise between the purity of sounds and versatility of an instrument.

---

Dynamic Transposition

With the invention of electronic instruments it is possible to combine the advantages of both rational and chromatic scales and avoid their drawbacks. Namely, one can make use of modulation. Modulation is usually understood as shift of a chord progression in a composition into a different key. Which, in physical terms, amounts to a shift in the frequency of all notes by a pre-defined factor, done during the composition. When this is done for a particular instrument for the whole duration of the composition, it is also called a transposition. But for a classical acoustic instrument, such as a piano or an organ it is virtually impossible to change the frequency of the sound produced by all keys during the performance. What we would like to to do is to transpose the instrument to any key during the performance, such that one can specify a key in which the instrument is playing for each measure of the composition.

Luckily, this can be easily accomplished for electronic instruments, that is, the shift in frequencies of all keys can be easily done at any time during the performance. Thus, we define dynamic transposition as a shift in frequency during the performance. On digital devices this can be accomplished by multiplication of the frequencies of all keys of an instrument by a pre-defined factor. Also, electronic instruments can play in any musical scale, not just the conventional chromatic scale. In particular, one can use a scale consisting of rational numbers described above, which is also known as just intonation scale. With this method one can play in any musical scale and retain the uniformity of musical intervals across the octaves, or indeed across any frequency ranges, by using a simple multiplication operation.

Let's illustrate this on an example. Suppose one wants to play a simple sequence of tones (a score) in four different keys. Let's compile the sequence from two harmonic triads, extended to fit two measures in 3/4 signature. Major sequence:

and minor:

where the sub-index identifies an octave. And the keys they are played in are:

(1)

C, Am, F, G

The whole composition score we want to play will be:

		C4, E4, G4, C5, G4, E4
(2)		A3, C4, E4, A4, E4, C4
		F3, A3, C4, F4, C4, A4
		G3, B3, D4, G4, D4, B3

which produces a familiar melodic sequence. Written in a conventional music notation it is:

And in a conventional piano-roll editor it will look like this:

Now, let's do the same with the dynamic transposition. The major sequence in rational scale is:

and for the minor sequence:

And the transposition sequence is:

which corresponds to (1) above. Then the composition score (2) becomes:

That's right - all four rows are almost identical, except some minor difference -). This is because the change of the key was taken care of by the transposition sequence. And here how it would look in a prototypical sequencer editor:

The piano keys are replaced with ratios corresponding to a nine-key scale: 1, 9/8, 6/5, 5/4, 4/3, 3/2, 8/5, 5/3, 9/5. Using this techniques one needs no more than a couple of octaves of keys to play any melody, since moving to other octaves will be done by the transposition sequence. For this one would add a transposition track to a song editor, like this:

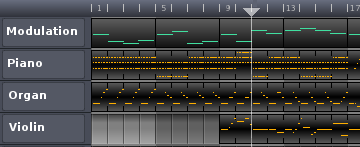
The transposition track can be entered in a similar manner as the score in the piano-roll editor above. A score for the transposition sequence will usually be simple, since it is just a sequence of harmonic keys for a song. Thus, the method simplifies writing an instrument score by replacing a complex score with a combination of a simpler score and an even simpler transposition sequence.

The additional simplicity comes from the fact that one does not have to know how to select the harmonic triads in different keys. This is because the octave does no longer have 12 semitones, out of which only 7 or so sound harmoneously. An octave is the scale! It can have only 7 tones, or less, if you are into simple scores, or as much as you like. Referring to the first diagram above, one does not need to know how to select red dots out of all the dots comprising an octave - there will only be red dots! All you need to remember, is which numbers "go well" with which numbers. For example to learn to play minor and major triads one should remember three numbers:

out of which the two basic combinations are build:

That's all one needs to remember. In contrast, in chromatic scale one has to remember how to select triples of notes out of 12 keys in an octave for each scale, thus producing: 12*2=24 different combinations for both minor and major keys.