
This document describes how one can write music using numbers. To do that we will create a simple text file with a music score for Pachelbel’s Canon in D.
Example files in the music notation described below can be found at these links: numeric notation (DTT) and mnemonic notation (DTM). Below we explain this notation in detail.

Here you see the beginning of the file where one can define some parameters and also provide comments after semi-columns. The first parameter is the base frequency, which in our case is the frequency of note D in the first octave.
Next you define seconds per beat. The composition is split into time intervals of different duration. The longest one is called measure which is sub-divided into beats. That’s why the next parameters specifies beats-per-measure. Beats are further split into ticks, so the next parameter specifies the number of ticks in a beat, and finally, ticks are split into picks.

Next we define our instruments or sounds. In this case we are using the standard sound font library where sounds are identified by numbers from the bank of sounds.
Each instrument is defined on one line starting with the
‘snd’ tag followed by the sound-font bank number for that
instrument and the name of the instrument that you gave it. One can pick
any name but here we are using a three-letter abbreviation for all
instruments for brevity. This particular composition is plaid on two
violins, viola, cello, and chorus.
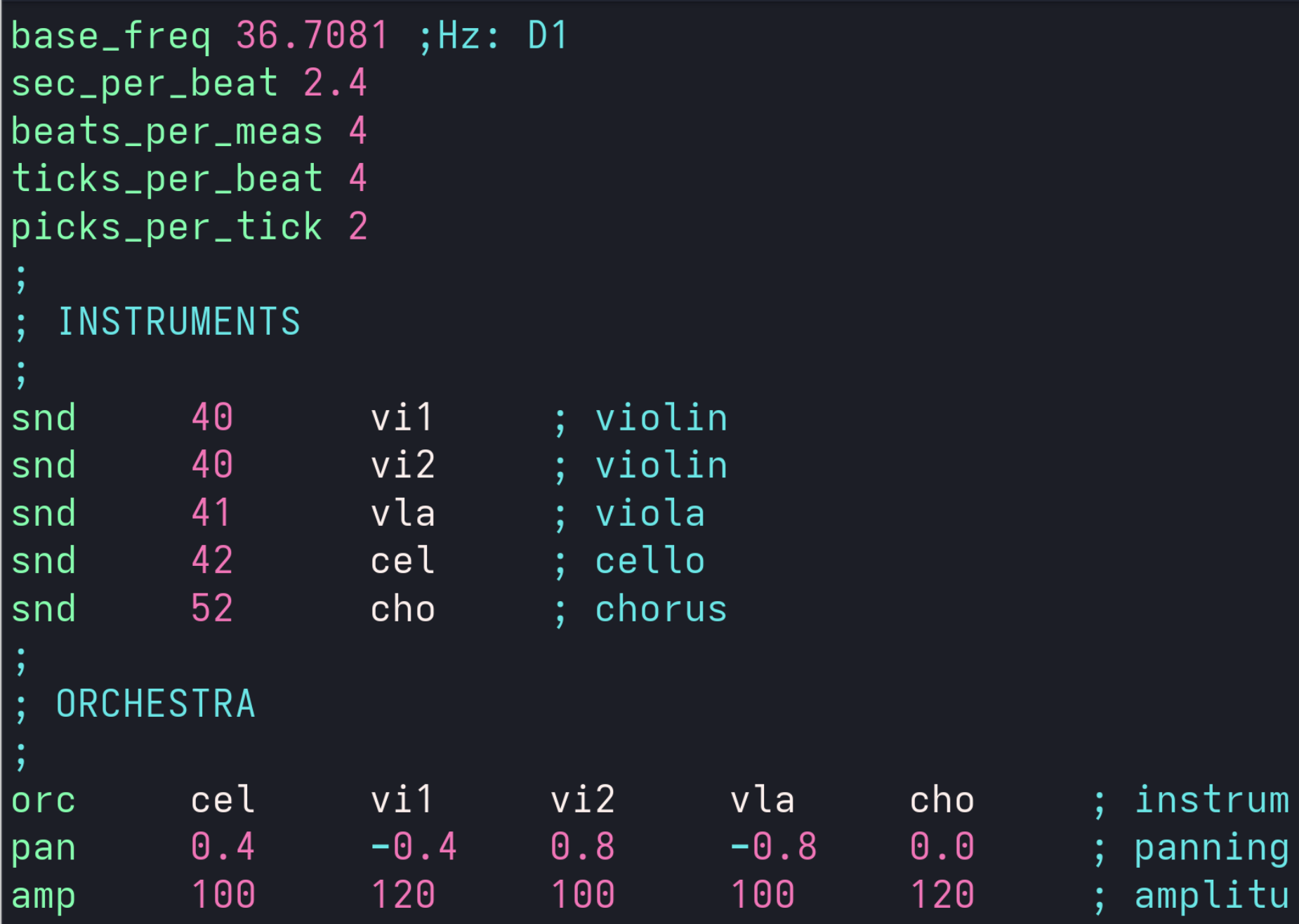
Next we combine our instruments into orchestra using a table. Each row of the table relates to a specific parameter identified by the tag in the beginning of the row.
The first row starts with the tag ‘orc’ and lists all the instruments in the orchestra by the names you assigned earlier.
The next row with the tag ‘pan’ provides pan value for each instrument placed under respective name of that instrument.
The final parameter is the initial volume or ‘amplitude’ provided in a similar manner for each instrument.

Now we can start writing the score. At the bottom we see the first beat of the first measure written as four lines - one line per tick.
The first pair of numbers on each line represents a fraction as
A:B = A/B. This fraction is used to multiply the base
frequency of the composition and apply it to the whole line. This will
be the base frequency of that line. In this case this fraction it is
simply one: 1:1=1/1=1. So the base frequency, of that line
will be equal to the base frequency of the composition which is D of the
first octave.
The subsequent triple of numbers on each line determine notes plaid
by respective instruments: the first two numbers define the fraction
that the base frequency of this line will be multiplied by and the third
one determines the octave. A dash sign means pause and a
plus sign means continuation of the sound from the line
above.
The octave number goes into the exponent of number 2. When we multiply any frequency by two raised to a number we shift the frequency to the octave equal to that number plus one. That’s why our octave numbers are equal to those on a piano minus one.
For example, the frequency of the first note plaid by the first instrument in our example is calculated as
base-frequency * 1 * 1 * 2 * 2 = 36.708 * 4 = 146.8
This produces frequency of note D in the third octave in a traditional notation.

Next figure shows the first measure with all for beats. The base frequency of each row in that beat is five-fourths of the composition’s base frequency which approximately corresponds to the interval between note D and F-sharp. Thus, the fourth beat is plaid in F#.
To calculate the frequency of the note plaid in the fourth beat, i.e. 6:5:1, we multiply the base frequency of the row by six-fifths and then by two raised to the power one. The result will be close to the frequency of note A in the second octave.
The first two measures of the composition are plaid by cello (01.mp3).
The second instrument, violin, joins cello in the third measure, and it’s notes are written in column 3.

This duet plays for another two measures (02.mp3).
After that the third instrument joins and so on.


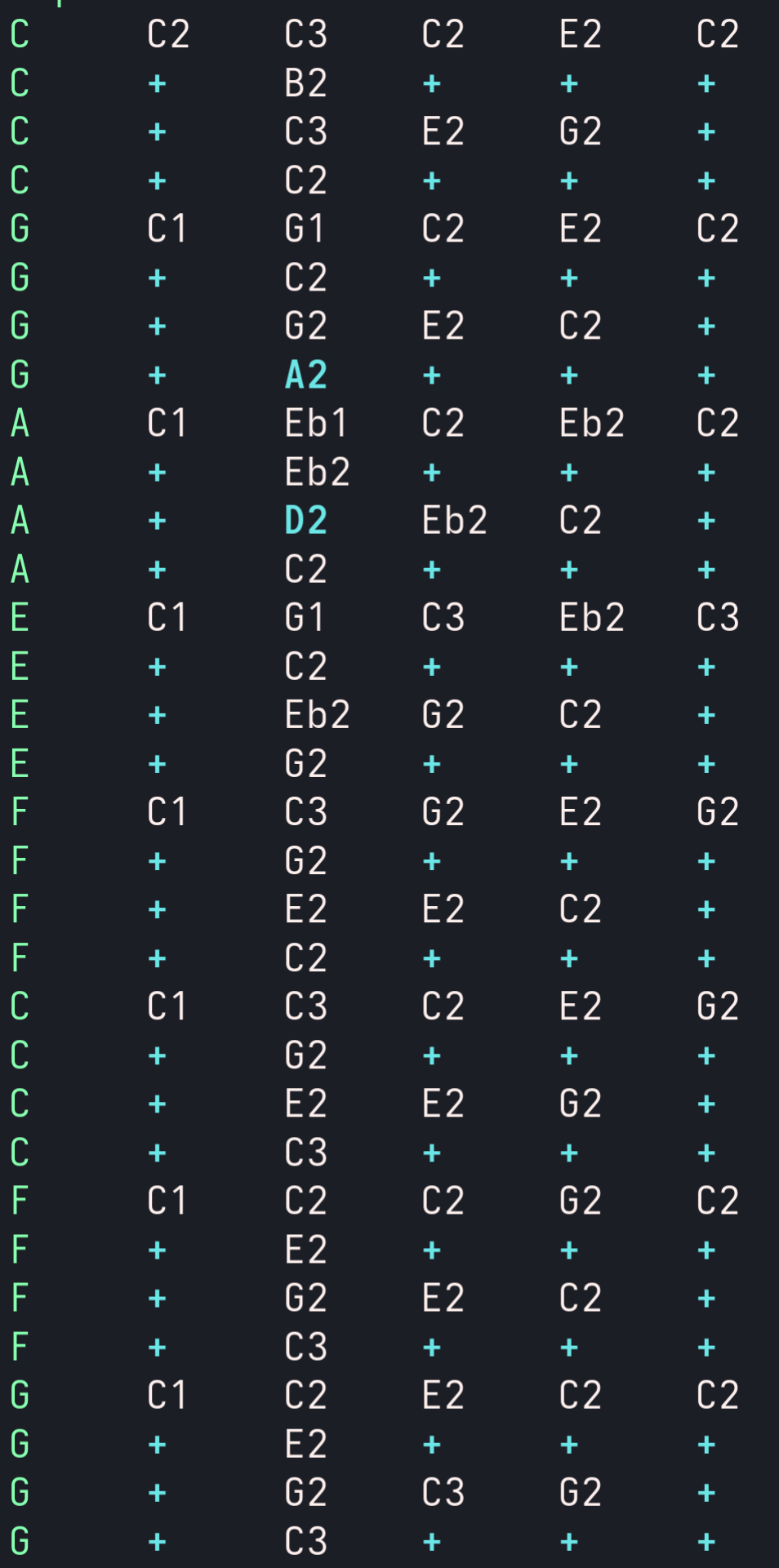
You might have noticed that there are only a few fractions used in the whole composition. This makes it possible to simplify the score by replacing all fractions with letters of your choice.
This can be easily done using definitions as shown in the next figure. Here we chose letters commonly used for notes in key C, just to follow the convention. With these definitions the score can be simplified and will look much cleaner. Next figure shows the example of the part plaid by five different instruments written in letter notation (03.mp3). We are still using octave numbers explicitly but all fractions are replaced with letters.
We chose to use letters that correspond to the key of C for convenience since that key has minimum of flats and sharps. And we wrote the score for the whole composition in five different keys: D, A, Bm, Fm, and G, using only notes in key C.
Think about this - we can play music in any key using only notes from key C !

In the proposed musical notation each line corresponds to a time interval smaller than one beat. These intervals were introduced earlier as ticks. But what if we want to start a note between the ticks? For this purpose we introduced picks which are time intervals smaller than a tick.
One can start a note at certain picks by using a dot or
comma notation. To start playing a note one pick before the
current tick one should append ".1" (dot-one) to the octave
number of this note, and to start the note two picks ahead of the next
tick one can append ",2" (comma-two) to the octave
number.
An example in the last figure shows the passage where the off-tick notes are used for the first violin. The corresponding music file is provided (04.mp3) along with a complete composition of Canon in D (canon.mp3) written in notation described here and rendered using the DTM Compiler.
Current implementation of the DTM Compiler converts the DTM score into either a MIDI file that can be plaid with FluidSynth using sound font library or can be converted to a CSound score file and plaid with CSound engine or converted to WAV or MP3 files.
Using this method one can simplify sequencing of music and produce more harmonious musical intervals. In particular:
One can play music in any key using only handful of notes, for example, only those from key C.
Music produced in this way is more harmonious because frequencies of notes are simple fractions of the base frequency, whereas in the standard Chromatic scale frequencies are defined by logarithmic transformation, producing intervals based on transcendental numbers.
Using rational numbers to set frequencies results in more harmonious musical intervals because this corresponds to harmonics of resonating strings. For more information please read the DTM Paper.