Zusammenfassung

Es wird eine Methode der Dynamischen Transposition für die Musiksequenzierung vorgestellt. Es vereinfacht das Komponieren von Musik durch die Verwendung rationaler Zahlen (siehe dieses Video) und erzeugt harmonischere musikalische Intervalle. Die Methode ist in einem Musiksequenzer implementiert, der über diesen Link und auf GitLab/andrei.v.smirnov/dtm verfügbar ist.

---

Rationale musikalische Skala

Die heute in der Musik weit verbreitete Chromatische Skala hat die Einschränkung, dass sie die Obertonreihe nicht exakt darstellen kann. Die Obertonreihe leitet sich von der Physik schwingender Saiten ab, die Grundfrequenzen sowie Obertöne oder Harmonische erzeugen. Die Frequenzen der Harmonischen unterscheiden sich um ganzzahlige Vielfache (z. B. 2, 3, 4, 5, ...). Diese Harmonischen überlagern sich und ergeben Frequenzen, die sich um verschiedene Brüche ganzer Zahlen unterscheiden, wie z. B. 1/2, 2/3, 3/4, 4/5, 5/6, ... sowie 3/2, 4/3, 5/4, 6/5 usw. Definitionsgemäß stellen diese Brüche Teilmengen der rationalen Zahlen dar.

Wenn die Frequenzen von Tönen durch solche harmonischen Multiplikatoren miteinander in Beziehung stehen, erzeugen sie tendenziell angenehme Klangkombinationen. Wenn sich beispielsweise die Grundfrequenzen dreier Töne in einem Verhältnis wie folgt bilden:

Sie klingen wie ein Dur-Akkord in chromatischer Tonleiter, z. B. C, E, G. Das entscheidende Wort ist hier ähnlich, da das tatsächliche Dur-Akkordverhältnis wie folgt lautet:

wobei die langen Zahlen oben das Ergebnis einer logarithmischen Operation sind und tatsächlich transzendente sind, wie die berühmte Zahl π. Dieser Unterschied scheint nicht signifikant zu sein. Bei einem Moll-Akkord ist er jedoch größer:

Andererseits lauten die rationalen Verhältnisse:

Und andere Töne einer chromatischen Tonleiter neigen dazu, noch weiter von der Rationalität abzuweichen, wie die folgende Grafik zeigt:

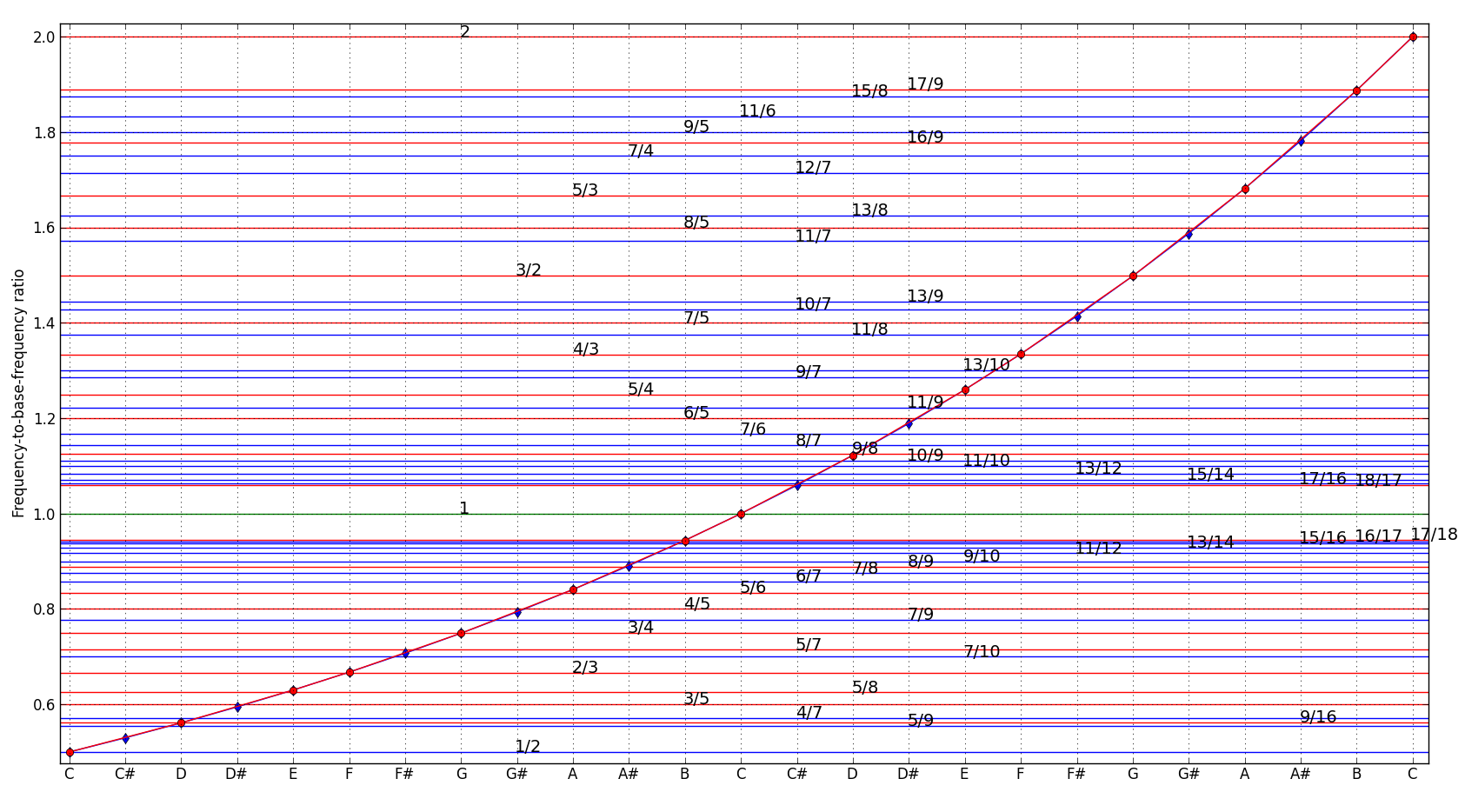
wobei rote Punkte auf der Kurve die Töne der chromatischen Tonleiter in C-Dur anzeigen. Die auf Frequenzen basierende Skala, die sich aus rationalen Zahlen ableiten, ist bekannt als "reine Stimmung" (just intonation). Hier bezeichnen wir sie als rationale Skala. Wie aus der Abbildung ersichtlich ist, stimmen die Frequenzen der rationalen Skala nur selten mit den Frequenzen der chromatischen Skala überein. Dies ist einer der Gründe, warum Akkorde auf einem elektronischen Keyboard weniger angenehm klingen als solche auf einem akustischen Klavier. Akustische Saiten können Resonanzeffekte aufweisen. Dadurch können sie ihre Frequenzen selbstständig aufeinander abstimmen und so von der chromatischen Stimmung zu angenehmeren rationalen Intervallen abweichen.

Die Entdeckung der rationalen Skala wird dem antiken griechischen Mathematiker Pythagoras zugeschrieben, der eine spezielle Teilmenge der rationalen Zahlen verwendete, die als Pythagoreische Skala bekannt ist. Die ersten Instrumente wurden nach dieser musikalischen Skala gebaut. Dies birgt jedoch ein Problem: die auf rationalen Zahlen basierende Töne zind nicht über die Oktaven hinweg einheitlich. Oktaven sind Frequenzbereiche, die mit dem Faktor der Zweierpotenz skaliert werden, d. h. 2ⁿ, wobei n eine ganze Zahl ist, wie z. B.: -4,-3,-2,-1,0,1,2,3,4, was in diesem Fall 9 Oktaven ergibt. Wenn man ein Instrument mit mehreren Oktaven oder einfach in verschiedenen Tonarten spielen und dabei in jeder Oktave ähnliche Klangkombinationen beibehalten möchte, lässt sich dies mit einer rationalen Skala nicht ohne Weiteres erreichen. Dies ist in der obigen Grafik zu sehen. Mit anderen Worten: In der pythagoreischen Tonleiter klingt dieselbe Melodie in verschiedenen Tonarten nicht gleich.

Deshalb wurde die chromatische Tonleiter als praktisches Mittel zum Bau eines auf Tasten basierenden Instruments entdeckt. Die chromatische Tonleiter stellt einen Kompromiss zwischen Klangreinheit und Vielseitigkeit eines Instruments dar.

---

Dynamische Transposition

Mit der Erfindung elektronischer Instrumente ist es möglich, die Vorteile rationaler und chromatischer Skalen zu kombinieren und deren Nachteile zu vermeiden. Insbesondere kann man Modulation verwenden. Modulation wird üblicherweise als Verschiebung einer Akkordfolge in einem Musikstück in eine andere Tonart verstanden. Physikalisch gesehen entspricht dies einer Verschiebung der Frequenzen aller Töne um einen vorher festgelegten Faktor, die während der Komposition erfolgt. Wenn dies für ein bestimmtes Instrument über die gesamte Dauer des Musikstücks geschieht, wird es auch als Transposition bezeichnet. Bei einem klassischen akustischen Instrument wie einem Klavier oder einer Orgel ist es jedoch praktisch unmöglich, die Frequenz des von allen Tasten erzeugten Tons während des Spielens zu verändern. Unser Ziel ist es, das Instrument während der Aufführung in jede beliebige Tonart zu transponieren, sodass man für jeden Takt des Musikstücks die Tonart festlegen kann, in der das Instrument spielt.

Zum Glück lässt sich dies bei elektronischen Instrumenten problemlos realisieren, das heißt, die Frequenzverschiebung aller Tonarten kann jederzeit während der Aufführung problemlos durchgeführt werden. Wir definieren daher dynamische Transposition als eine globale Frequenzverschiebung während der Aufführung. Bei digitalen Geräten kann dies durch Multiplikation der Frequenzen aller Tasten eines Instruments mit einem vordefinierten Faktor erreicht werden. Elektronische Instrumente können außerdem in jeder beliebigen Tonleiter spielen, nicht nur in der herkömmlichen chromatischen Tonleiter. Insbesondere kann man eine Skala verwenden, die aus rationalen Zahlen besteht, wie oben beschrieben, die auch als reine Stimmung-Skala bekannt ist. Mit dieser Methode kann man in jeder beliebigen Tonleiter spielen und die Gleichmäßigkeit der musikalischen Intervalle über die Oktaven oder sogar über beliebige Frequenzbereiche hinweg beibehalten, indem man eine einfache Multiplikationsoperation anwendet.

Lassen Sie uns dies an einem Beispiel veranschaulichen. Angenommen, man möchte eine einfache Tonfolge (eine Partitur) in vier verschiedenen Tonarten spielen. Wir kompilieren die Sequenz aus zwei harmonischen Dreiklängen, erweitert auf zwei Takte im 3/4-Takt. Hier ist eine melodische Sequenz in Dur:

Und hier ist eine melodische Sequenz in Moll:

wobei der Subindex eine Oktave kennzeichnet. Und die Tonarten, in denen die melodischen Sequenzen gespielt werden, sind:

(1)

C, Am, F, G

Die vollständige Partitur, die wir spielen möchten, lautet:

		C4, E4, G4, C5, G4, E4
(2)		A3, C4, E4, A4, E4, C4
		F3, A3, C4, F4, C4, A4
		G3, B3, D4, G4, D4, B3

Dadurch entsteht eine bekannte Melodiefolge, die in herkömmlicher Musiknotation wie folgt geschrieben wird:

Und ein Piano-Roll-Editor sieht dann so aus:

Nun machen wir das Gleiche mit der dynamischen Transposition. Die melodische Sequenz in Dur in rationaler Tonleiter lautet:

Und für die melodische Sequenz in Moll haben wir:

Und die Transpositionsfolge lautet:

was dem oben genannten (1) entspricht. Dann ergibt sich die Kompositionsnote (2) zu:

Das stimmt – alle vier Reihen sind fast identisch, abgesehen von einigen kleinen Unterschieden. Dies liegt daran, dass die Änderung der Tonart durch die Transpositionssequenz übernommen wurde. Und so würde es in einem prototypischen Sequenzer-Editor aussehen:

Die Klaviertasten werden durch Verhältnisse ersetzt, die einer Neun-Tasten-Tonleiter entsprechen: 1, 9/8, 6/5, 5/4, 4/3, 3/2, 8/5, 5/3, 9/5. Mit dieser Technik benötigt man zum Spielen jeder beliebigen Melodie nicht mehr als ein paar Oktaven an Tasten, da der Wechsel in andere Oktaven durch die Transpositionssequenz erfolgt. Dazu würde man im Song-Editor eine Transpositionsspur hinzufügen, etwa so:

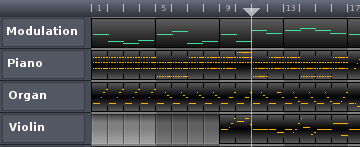
Die Transpositionsspur kann auf ähnliche Weise wie die Partitur im oben genannten Piano-Roll-Editor eingegeben werden. Die Partitur für die Transpositionssequenz ist in der Regel einfach, da es sich lediglich um eine Folge harmonischer Tonarten für ein Lied handelt. Die Methode vereinfacht somit das Schreiben einer Instrumentalpartitur, indem sie eine komplexe Partitur durch eine Kombination aus einer einfacheren Partitur und einer noch einfacheren Transpositionssequenz ersetzt.

Die zusätzliche Einfachheit ergibt sich daraus, dass man nicht wissen muss, wie man die harmonischen Dreiklänge in verschiedenen Tonarten auswählt. Dies liegt daran, dass die Oktave nicht mehr aus 12 Halbtönen besteht, von denen nur etwa 7 harmonisch klingen. Eine Oktave ist die musikalische Tonleiter! Es kann nur 7 Töne haben, oder weniger, wenn Sie einfache Partituren bevorzugen, oder so viele, wie Sie möchten. Bezüglich des ersten Diagramms oben muss man nicht wissen, wie man die roten Punkte aus allen Punkten einer Oktave auswählt – es gibt nur rote Punkte! Sie müssen sich lediglich merken, welche Zahlen „gut zusammenpassen“. Um beispielsweise das Spielen von Moll- und Dur-Dreiklängen zu erlernen, sollte man sich drei Zahlen merken:

Aus denen die beiden Grundkombinationen gebildet werden:

Und so werden sie in jeder Tonart notiert! Das ist alles, was man wissen muss. Im Gegensatz dazu muss man sich bei der chromatischen Tonleiter merken, wie man in einer Oktave für jede Tonleiter Triolen aus 12 Tonarten auswählt, wodurch sich 12*2=24 verschiedene Kombinationen sowohl für Moll- als auch für Dur-Tonarten ergeben.