Résumé

Une méthode de transposition dynamique pour le séquençage musical est présentée. Cette méthode simplifie l'écriture musicale en utilisant des nombres rationnels et produit des intervalles musicaux plus harmonieux. (Regardez cette vidéo). La méthode est implémentée dans un séquenceur musical disponible via ce lien et sur GitLab/andrei.v.smirnov/dtm.

---

Échelle musicale rationnelle

La gamme chromatique standard, largement utilisée en musique aujourd'hui, présente la limitation de ne pas pouvoir représenter exactement les séries harmoniques . La série harmonique est issue de la physique des cordes résonnantes qui produisent des fréquences fondamentales ainsi que des harmoniques. overtones. Les fréquences des harmoniques diffèrent par des multiplicateurs entiers (c'est-à-dire 2, 3, 4, 5, ...). Ces harmoniques se superposent pour produire des fréquences qui diffèrent par diverses fractions construites à partir de nombres entiers, telles que 1/2, 2/3, 3/4, 4/5, 5/6, ... ainsi que 3/2, 4/3, 5/4, 6/5, etc. Par définition, ces fractions représentent des sous-ensembles des nombres rationnels.

Lorsque les fréquences des sons sont liées entre elles par de tels multiplicateurs harmoniques, elles tendent à produire des combinaisons sonores agréables. Par exemple, si les fréquences fondamentales de trois sons forment un rapport comme:

Elles sonneront comme un accord majeur dans une gamme chromatique, par exemple C, E, G. Le mot important ici est comme. Le rapport réel des accords majeurs sera:

où les longs nombres ci-dessus sont le résultat d'une opération logarithmique et sont en fait transcendantaux, comme le célèbre nombre π. Cette différence ne semble pas significative. Cependant, pour un accord mineur, il sera plus grand:

Et les rapports rationnels les plus proches sont :

D'autres tonalités d'une gamme chromatique tendent à s'éloigner encore davantage de la rationalité, comme le montre le graphique ci-dessous:

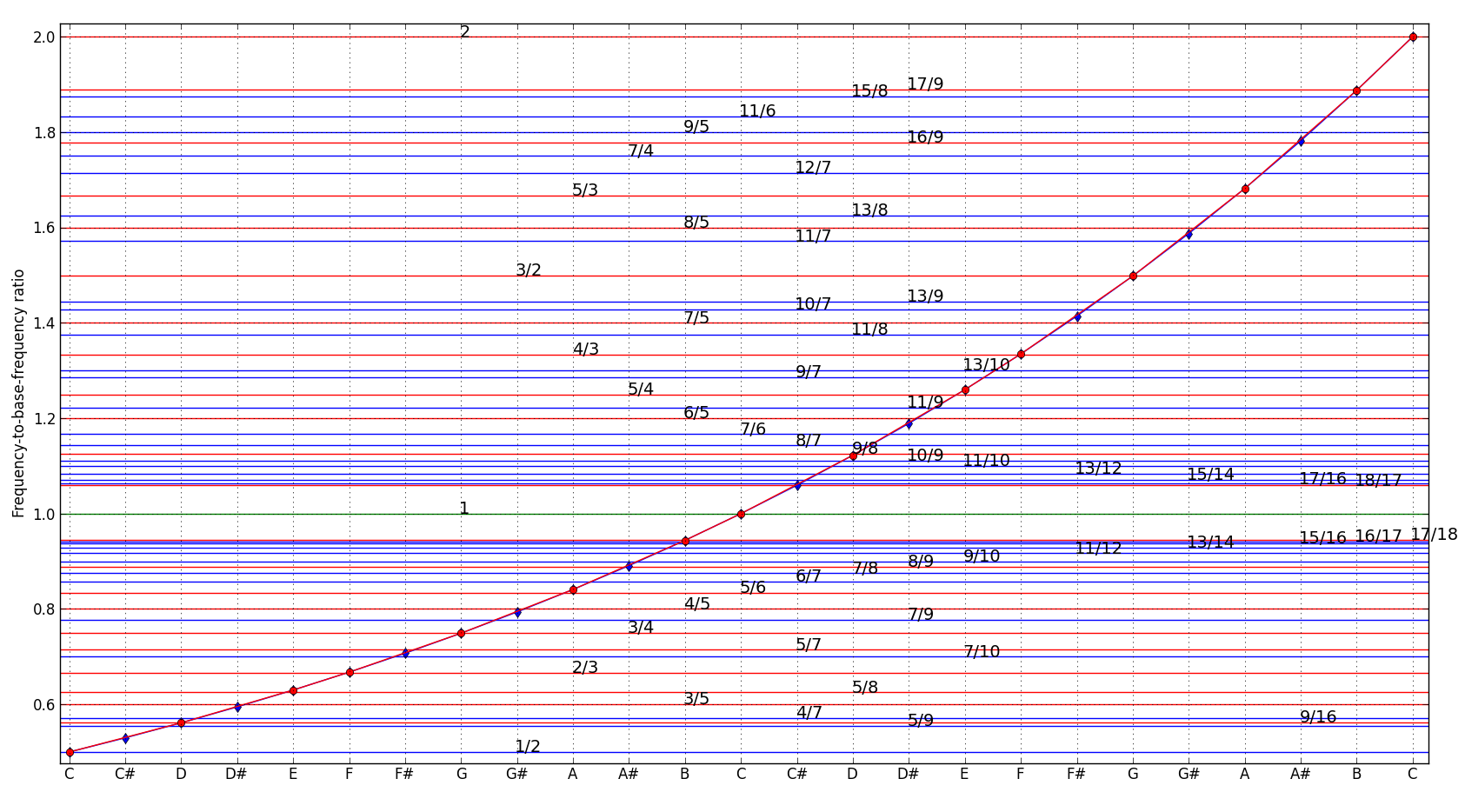
où les points rouges sur la courbe indiquent les notes de la gamme chromatique en do majeur (C). L'échelle basée sur des fréquences dérivées de nombres rationnels est connue sous le nom de échelle d'intonation juste. Nous l'appellerons ici une échelle rationnelle. Comme on peut le constater sur la figure, les fréquences de l'échelle rationnelle correspondent rarement aux fréquences de l'échelle chromatique. C’est l’une des raisons pour lesquelles les accords joués sur un clavier électronique sonnent moins agréablement que ceux joués sur un piano acoustique. Les cordes acoustiques peuvent subir un effet de résonance. De ce fait, ils peuvent auto-ajuster leurs fréquences l'une à l'autre, passant ainsi d'un accordage chromatique à des intervalles rationnels plus agréables.

La découverte de l'échelle rationnelle est attribuée à un mathématicien grec antique, Pythagore qui utilisait un sous-ensemble spécifique de nombres rationnels connu sous le nom d'échelle pythagoricienne. Les instruments précédents étaient construits à cette échelle. Cependant, il présente également un problème. En effet, la gamme construite sur les nombres rationnels n'est pas uniforme sur toutes les octaves. Les octaves sont les plages de fréquences mises à l'échelle par le facteur de la puissance de deux, c'est-à-dire 2ⁿ, avec n étant un nombre entier comme : -4,-3,-2,-1,0,1,2,3,4, ce qui produira 9 octaves. Si l'on souhaite jouer d'un instrument à plusieurs octaves, ou simplement dans des tonalités différentes, tout en conservant des combinaisons sonores similaires dans chaque octave, on ne peut pas y parvenir facilement avec une gamme rationnelle. Cela est visible sur le graphique ci-dessus. Autrement dit, dans la gamme pythagoricienne, une même mélodie jouée dans des tonalités différentes ne sonnera pas de la même manière.

C’est pourquoi la gamme chromatique a été découverte comme un moyen pratique de construire un instrument à touches. Ainsi, la gamme chromatique représente un compromis entre la pureté des sons et la polyvalence d'un instrument.

---

Transposition dynamique

With the invention of electronic instruments it is possible to combine the advantages of both rational and chromatic scales and avoid their drawbacks. On peut également utiliser la modulation. La modulation est généralement comprise comme le déplacement d'une progression d'accords. Ce qui, en termes physiques, équivaut à un décalage de la fréquence de toutes les notes d'un facteur prédéfini, effectué lors de la composition. Lorsque cela est fait pour un instrument particulier pendant toute la durée de la composition, on parle également de transposition. Mais pour un instrument acoustique classique, comme un piano ou un orgue, il est pratiquement impossible de modifier la fréquence du son produit par toutes les touches pendant l'exécution. Ce que nous souhaitons faire, c'est transposer l'instrument dans n'importe quelle tonalité pendant l'exécution, de sorte que l'on puisse spécifier la tonalité dans laquelle l'instrument joue pour chaque mesure de la composition.

Heureusement, cela peut être facilement réalisé pour les instruments électroniques, c'est-à-dire que le changement de fréquence de toutes les tonalités peut être effectué facilement à tout moment pendant l'exécution. Ainsi, nous définissons la transposition dynamique comme un changement de fréquence pendant l'exécution. Sur les appareils numériques, cela peut être réalisé en multipliant les fréquences de toutes les touches d'un instrument par un facteur prédéfini. De plus, les instruments électroniques peuvent jouer dans n'importe quelle gamme musicale, et pas seulement dans la gamme chromatique conventionnelle . En particulier, on peut utiliser une échelle composée de nombres rationnels décrite ci-dessus, également connue sous le nom d'échelle d'intonation juste . Grâce à cette méthode, on peut jouer dans n'importe quelle gamme musicale et conserver l'uniformité des intervalles musicaux sur toutes les octaves, voire sur toutes les plages de fréquences, en utilisant une simple opération de multiplication.

Illustrons cela par un exemple. Suppose one wants to play a simple sequence of tones (a score) in four different keys. Compilons la séquence à partir de deux triades harmoniques, étendues pour tenir sur deux mesures en 3/4 signature. Séquence majeure:

et séquence mineure:

où le sous-indice identifie une octave. Les tonalités musicales dans lesquelles la séquence de notes est jouée sont:

(1)

C, Am, F, G

La partition complète que nous souhaitons jouer sera:

		C4, E4, G4, C5, G4, E4
(2)		A3, C4, E4, A4, E4, C4
		F3, A3, C4, F4, C4, A4
		G3, B3, D4, G4, D4, B3

qui produit une séquence mélodique familière. Écrit en notation musicale conventionnelle, cela donne:

Et dans un éditeur de type piano roll classique, cela ressemblera à ceci:

Maintenant, faisons de même avec la transposition dynamique. La séquence principale à l'échelle rationnelle est:

et pour la séquence mineure est:

Et la séquence de transposition est:

ce qui correspond à (1) ci-dessus. La partition de composition (2) devient alors:

C'est exact - les quatre rangées sont presque identiques, à quelques petites différences près -). Ceci s'explique par le fait que le changement de tonalité a été pris en charge par la séquence de transposition. Voici à quoi cela ressemblerait dans un prototype d'éditeur de séquenceur:

Les touches du piano sont remplacées par des rapports correspondant à une gamme à neuf touches : 1, 9/8, 6/5, 5/4, 4/3, 3/2, 8/5, 5/3, 9/5. Grâce à ces techniques, il suffit de quelques octaves de touches pour jouer n'importe quelle mélodie, puisque le passage à d'autres octaves se fera par la séquence de transposition. Pour cela, il faudrait ajouter une piste de transposition à un éditeur de chansons, comme ceci:

La piste de transposition peut être saisie de la même manière que la partition dans l'éditeur de piano roll ci-dessus. La partition de la séquence de transposition est généralement simple, puisqu'il s'agit simplement d'une suite de tonalités harmoniques pour une chanson. La partition de la séquence de transposition est généralement simple, puisqu'il s'agit simplement d'une suite de tonalités harmoniques pour une chanson. Ainsi, la méthode simplifie l'écriture d'une partition instrumentale en remplaçant une partition complexe par une combinaison d'une partition plus simple et d'une séquence de transposition encore plus simple.

Cette simplicité supplémentaire provient du fait qu'il n'est pas nécessaire de savoir comment sélectionner les triades harmoniques dans différentes tonalités. Ceci s'explique par le fait que l'octave ne comporte plus 12 demi-tons, dont seulement 7 environ sonnent harmonieusement. Une octave est la gamme ! Elle peut ne comporter que 7 notes, ou moins, si vous préférez les partitions simples, ou autant que vous le souhaitez. En se référant au premier diagramme ci-dessus, il n'est pas nécessaire de savoir comment sélectionner les points rouges parmi tous les points composant une octave - il n'y aura que des points rouges ! Il vous suffit de retenir quels nombres «s'accordent bien» avec quels autres nombres. Par exemple, pour apprendre à jouer des triades mineures et majeures, il faut se souvenir de trois chiffres :

à partir desquelles sont construites les deux combinaisons de base :

C'est tout ce qu'il faut retenir. En revanche, dans la gamme chromatique, il faut se souvenir comment sélectionner des triplets de notes parmi les 12 tonalités d'une octave pour chaque gamme, produisant ainsi : 12*2=24 combinaisons différentes pour les tonalités mineures et majeures.